Grids and maps

Volumetric grid

Introduction

Macromolecular models are often accompanied by 3D data on an evenly spaced, rectangular grid (but note that the spacing in different directions may differ). The data may represent electron density, a mask of the protein area, or any other scalar data.

In Gemmi such a data is stored in a class called Grid. Actually, it is a set of classes for storing different types of data: floating point numbers, integers or boolean masks.

Grid dimension are given in variables nu, nv, nw. The data layout is Fortran-style contiguous, i.e. point (1,1,1) is followed by (2,1,1).

Grid classes also store:

• unit cell dimensions (to know Cartesian coordinates of grid nodes),

• and crystallographic symmetry (to know symmetry-equivalent grid nodes).

If the symmetry is not set (or is set to P1) we effectively have a box with periodic boundary conditions (PBC).

C++

The gemmi/grid.hpp header defines:

template<typename T=float> struct Grid;

which stores dimensions and data:

int nu, nv, nw;
std::vector<T> data;

To specify the grid size use function set_size() or set_size_from_spacing(). They both check that the size is compatible with the space group (so it is better to call these functions after setting Grid::spacegroup. The latter function additionally ensures that the size is FFT-friendly.

The data point can be accessed with:

T Grid<T>::get_value(int u, int v, int w) const
void Grid<T>::set_value(int u, int v, int w, T x)

(This class has a number of other functions that are not documented yet. The majority of Gemmi users use it from Python, so that’s also where most of the documentation effort goes.)

Python

In Python we have classes FloatGrid (for maps), Int8Grid (for masks). (We will add other classes such and ComplexGrid when we see a use for it.)

The constructor may take grid dimensions or a NumPy array as an argument:

>>> import gemmi
>>> grid = gemmi.FloatGrid(12, 12, 12)
>>> grid.nu, grid.nv, grid.nw
(12, 12, 12)

>>> grid2 = gemmi.FloatGrid(numpy.zeros((30, 31, 32), dtype=numpy.float32))
>>> grid2.nu, grid2.nv, grid2.nw
(30, 31, 32)

Alternatively, you may set (or change) the size later on:

>>> grid3 = gemmi.FloatGrid()
>>> # grid3.spacegroup = ...
>>> grid3.set_size(12, 12, 12)

The advantage of calling set_size() after a space group was set is that this function checks if the size is compatible with the space group (a symmetry operation cannot map a node to a point between nodes).

If a unit cell is assigned to the grid (it will be discussed later), you can request the size that gives approximately the specified spacing, with one of the possible rounding modes: Nearest, Up (denser grid) and Down:

>>> grid3.set_unit_cell(gemmi.UnitCell(40, 50, 40, 90, 82.5, 90))
>>> grid3.set_size_from_spacing(1.2, gemmi.GridSizeRounding.Nearest)

You can create a copy of a grid with:

>>> grid.clone()
<gemmi.FloatGrid(12, 12, 12)>

Values are accessed with functions get_value() and set_value():

>>> grid.set_value(1, 1, 1, 7.0)
>>> grid.get_value(1, 1, 1)
7.0
>>> # we can test wrapping of indices (a.k.a. periodic boundary conditions)
>>> grid.get_value(-11, 13, 25)
7.0

The data can be also accessed through the buffer protocol. It means that you can use it as a NumPy array (Fortran-style contiguous) without copying the data:

>>> import numpy
>>> array = numpy.array(grid, copy=False)
>>> array.dtype
dtype('float32')
>>> array.shape
(12, 12, 12)
>>> numpy.argwhere(array == 7.0)
array([[1, 1, 1]])

The buffer protocol is not specific to NumPy – any other Python library that supports this protocol can directly access the grid data. Alternatively, the grid can be viewed as a NumPy array through the array property:

>>> grid.array.shape
(12, 12, 12)

Symmetry

The main advantage that Grid has over a generic 3D array is that it understands crystallographic symmetry. After setting the symmetry we can use a family of symmetrize functions that performs operations on symmetry-equivalent grid points. For example, we can set all equivalent points to the value calculated as a minimum, maximum or a sum of values of the equivalent points.

In C++ we directly set the spacegroup property:

const SpaceGroup* spacegroup;

Similarly in Python:

>>> grid.spacegroup = gemmi.find_spacegroup_by_name('P2')

Now let us use one of the symmetrizing functions:

>>> # the point (1, 1, 1) was already set to 7.0
>>> grid.set_value(0, 0, 0, 0.125)  # a special position
>>> grid.sum()  # for now only two points: 7.0 + 0.125
7.125
>>> grid.symmetrize_max()  # applying symmetry
>>> grid.sum()  # one point got duplicated, the other is on rotation axis
14.125

In C++ we have a templated function that can perform any operation on symmetry-equivalent points:

template<typename Func> void Grid::symmetrize(Func func)

Python bindings provide the following specializations:

>>> grid.symmetrize_min()      # minimum of equivalent values
>>> grid.symmetrize_max()      # maximum
>>> grid.symmetrize_abs_max()  # max(|x|)
>>> grid.symmetrize_avg()      # average
>>> grid2.symmetrize_sum()     # sum (symmetry-equivalent nodes are added, multiplying nodes on special positions)

Unit cell

The unit cell parameters (in a member variable unit_cell: UnitCell) enable conversion between coordinates and grid points.

The unit cell should be set using Grid<T>::set_unit_cell(), which in addition to setting unit_cell sets also spacing, the spacing between grid planes that is precalculated for efficiency.

>>> grid.set_unit_cell(gemmi.UnitCell(45, 45, 45, 90, 82.5, 90))
>>> grid.unit_cell
<gemmi.UnitCell(45, 45, 45, 90, 82.5, 90)>
>>> grid.spacing  
(3.7179..., 3.75..., 3.7179...)

Each grid point (u, v, w) can now be expressed in fractional or Cartesian coordinates:

>>> grid.get_fractional(6, 6, 6)
<gemmi.Fractional(0.5, 0.5, 0.5)>
>>> grid.get_position(6, 6, 6)
<gemmi.Position(25.4368, 22.5, 22.3075)>

Grid point

Grid contains a little helper class (GridBase<T>::Point in C++) that bundles grid point coordinates (u, v, w: int) and a pointer to the value in grid (value). This bundle is obtained with getter:

>>> grid.get_point(0, 0, 0)
<gemmi.FloatGridBase.Point (0, 0, 0) -> 0.125>
>>> _.u, _.v, _.w, _.value
(0, 0, 0, 0.125)

or when iterating the grid:

>>> for point in grid:
...   if point.value != 0.: print(point)
<gemmi.FloatGridBase.Point (0, 0, 0) -> 0.125>
<gemmi.FloatGridBase.Point (1, 1, 1) -> 7>
<gemmi.FloatGridBase.Point (11, 1, 11) -> 7>

The point can be converted to its index (position in the array):

>>> point = grid.get_point(6, 6, 6)
>>> grid.point_to_index(point)
942

to fractional coordinates:

>>> grid.point_to_fractional(point)
<gemmi.Fractional(0.5, 0.5, 0.5)>

and to orthogonal (Cartesian) coordinates in Angstroms:

>>> grid.point_to_position(point)
<gemmi.Position(25.4368, 22.5, 22.3075)>

The other way around, we can find the grid point nearest to a position:

>>> grid.get_nearest_point(_)
<gemmi.FloatGridBase.Point (6, 6, 6) -> 0>

Common operations

We have a helper function to copy the spacegroup and unit cell from a macromolecular structure (Structure):

>>> new_grid = gemmi.FloatGrid()
>>> st = gemmi.read_structure('../tests/1orc.pdb')
>>> new_grid.setup_from(st)

---

The Grid class is often used for electron density maps. A common operation on such maps is normalization – scaling that changes the mean to 0 and RMSD to 1:

>>> gr = grid.clone()
>>> gr.normalize()

---

To extract a block-shaped sub-array data as a Fortran-contiguous array, or to set data in a block in a grid, use functions get/set_subarray. Unlike array slicing, these functions are aware of the cell repeat (PBC) – the block area is not limited by the unit cell boundaries.

>>> sub = gr.get_subarray(start=[3,3,3], shape=[2,3,4])
>>> sub.shape
(2, 3, 4)
>>> gr.set_subarray(sub, start=[0,0,0])

---

To set the whole grid to the same value use:

>>> gr.fill(0)

To set the grid points in a certain radius from a specified position use:

void Grid<T>::set_points_around(const Position& ctr, double radius, T value)

>>> gr.set_points_around(gemmi.Position(25, 25, 25), radius=3, value=10)
>>> numpy.argwhere(gr.array == 10)
array([[6, 6, 7],
       [6, 7, 7]])

This function, to be efficient, ignores symmetry. At the end we should call one of the symmetrizing functions:

>>> gr.symmetrize_max()

While we could use the above functions for masking the molecule (or bulk solvent) area, we have specialized functions to create a bulk solvent mask.

Interpolation

To get a value corresponding to an arbitrary position, you may use trilinear interpolation of the 8 nearest nodes, or tricubic interpolation that uses 64 nodes.

C++

T Grid<T>::interpolate_value(const Fractional& fctr) const
T Grid<T>::interpolate_value(const Position& ctr) const

double Grid<T>::tricubic_interpolation(const Fractional& fctr) const
double Grid<T>::tricubic_interpolation(const Position& ctr) const

// calculates also derivatives
std::array<double,4> Grid<T>::tricubic_interpolation_der(double x, double y, double z) const

Python

>>> grid.interpolate_value(gemmi.Fractional(1/24, 1/24, 1/24))
0.890625
>>> grid.interpolate_value(gemmi.Position(2, 3, 4))
2.0333263874053955
>>> grid.tricubic_interpolation(gemmi.Fractional(1/24, 1/24, 1/24))
1.283477783203125
>>> grid.tricubic_interpolation(gemmi.Position(2, 3, 4))  
2.6075661737715...
>>> # calculate also derivatives in directions of unit cell axes
>>> grid.tricubic_interpolation_der(gemmi.Fractional(1/24, 1/24, 1/24))
[1.283477783203125, 35.523193359375, 36.343505859375, 35.523193359375]

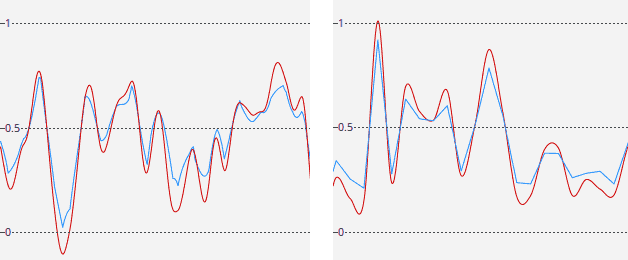
The cubic interpolation is smoother than linear, but may amplify the noise. This is illustrated on the plots below, which shows density along two lines in a grid that was filled with random numbers from [0, 1). Trilinear interpolation is blue, tricubic – red. The left plot shows density along a line in a random direction, the right plot – along a line parallel to one of the axes.

Implementation notes

Tricubic interpolation, as described on Wikipedia page and in Appendix B of a PHENIX paper, can be implemented either as 21 cubic interpolations, or using method introduced by Lekien & Marsen in 2005, which involves 64x64 matrix of integral coefficients (see also this blog post). The latter method should be more efficient, but gemmi uses the former, which takes ~100 ns. If you’d like to speed it up or to get derivatives, contact developers.

Optimization for Python

If you have a large number of points, making a Python function call each time would be slow. If these points are on a regular 3D grid (which may not be aligned with our grid) call interpolate_values() (with s at the end) with two arguments: a 3D NumPy array (for storing the results) and a Transform that relates indices of the array to positions in the grid:

>>> # first we create a numpy array of the same type as the grid
>>> arr = numpy.zeros([32, 32, 32], dtype=numpy.float32)
>>> # then we setup a transformation (array indices) -> (position [A]).
>>> tr = gemmi.Transform()
>>> tr.mat.fromlist([[0.1, 0, 0], [0, 0.1, 0], [0, 0, 0.1]])
>>> tr.vec.fromlist([1, 2, 3])
>>> # finally we calculate interpolated values
>>> grid.interpolate_values(arr, tr)
>>> arr[10, 10, 10]  # -> corresponds to Position(2, 3, 4)
2.0333264

(If your points are not on a regular grid – get in touch – there might be another way.)

ASU and MaskedGrid

Sometimes we want to focus on a part of the grid only. For this, we have class MaskedGrid that contains vector marking masked positions and a reference to the original grid.

When an element of the mask is 0 (false), the corresponding element of the grid is unmasked and is to be used. This is the same convention as in NumPy MaskedArray.

The primary use for MaskedGrid is working with asymmetric unit (asu) only:

>>> asu = grid.masked_asu()
>>> asu  
<gemmi.MaskedFloatGrid object at 0x...>
>>> asu.grid is grid
True
>>> asu.mask_array  
array([[[0, 0, 0, ..., 1, 1, 1],
       ...
        [1, 0, 0, ..., 1, 1, 1]]], dtype=int8)
>>> sum(point.value for point in asu)
7.125
>>> for point in asu:
...   if point.value != 0: print(point)
<gemmi.FloatGridBase.Point (0, 0, 0) -> 0.125>
<gemmi.FloatGridBase.Point (1, 1, 1) -> 7>

Solvent mask

Gemmi implements a variant of the most popular method for calculating the bulk solvent area. This method was introduced in CNS. It uses van der Waals (or similar) atomic radii r and two parameters: r_probe and r_shrink.

• We mark the area in radius r + r_probe of each atom as non-solvent (0). r usually depends on the element, but some programs use the same radius for all atoms. The extra margin r_probe is largely cancelled in the next step.

• We shrink the non-solvent area by r_shrink. All the 0’s in a distance r_shrink from 1’s are changed to 1, shrinking the solvent volume. Both r_probe and r_shrink have the same order of magnitude. Jiang & Brünger (1994) proposed r_probe = 1.0 Å and r_shrink = 1.1 Å.

• The above procedure eliminates small solvent islands. If it is not sufficient, we can explicitly remove islands (contiguous areas of 1’s) up to a certain volume. This step was added for compatibility with Refmac.

Here is how to create a mask identical as phenix.mask:

>>> masker = gemmi.SolventMasker(gemmi.AtomicRadiiSet.Cctbx)
>>> st = gemmi.read_structure('../tests/1orc.pdb')
>>> grid = gemmi.Int8Grid()
>>> # take space group and unit cell from Structure,
>>> # and set size based on the specified minimal spacing
>>> grid.setup_from(st, spacing=0.6)
>>> masker.put_mask_on_int8_grid(grid, st[0])

The parameters of SolventMasker can be inspected and changed:

>>> masker.atomic_radii_set
<AtomicRadiiSet.Cctbx: 1>
>>> masker.rprobe
1.1
>>> masker.rshrink
0.9
>>> masker.island_min_volume  # 0 = unused
0.0
>>> masker.constant_r  # 0 = unused
0.0

The example above uses a parameter set based on cctbx. We also have a few others sets. You can create mask similar to Refmac (but due to unintended features of solvent masking in Refmac, the results are not identical):

>>> masker = gemmi.SolventMasker(gemmi.AtomicRadiiSet.Refmac)

or a mask with Van der Waals radii from Wikipedia and r_probe = 1.0 Å and r_shrink = 1.1 Å, as in the original Jiang & Brünger paper:

>>> masker = gemmi.SolventMasker(gemmi.AtomicRadiiSet.VanDerWaals)

or with constant radius, similarly to the NCSMASK program from CCP4:

>>> masker = gemmi.SolventMasker(gemmi.AtomicRadiiSet.Constant, 3.0)

If the mask is to be FFT-ed to structure factors, store it on FloatGrid (function put_mask_on_float_grid in Python and put_mask_on_grid in C++). See the section about bulk solvent coorection for details and examples.

Blob search

When we have an electron density map on a Grid we may want to check blobs – unmodelled electron density, potential ligand sites. Similarly to the “Unmodelled blobs” function in COOT, Gemmi has a function that finds such blobs. It was added to be used in CCP4 Dimple.

The blobs can be searched either in a difference map, or in a normal map with the model masked out. In this example we do the latter.

>>> # load map from MTZ
>>> mtz = gemmi.read_mtz_file('../tests/5wkd_phases.mtz.gz')
>>> grid = mtz.transform_f_phi_to_map('FWT', 'PHWT', sample_rate=3)
>>>
>>> # Load model. No real blobs in this tiny example,
>>> # so we remove water to get one water-sized blob.
>>> st = gemmi.read_structure('../tests/5wkd.pdb')
>>> st.remove_waters()
>>>
>>> # use SolventMasker to mask the models with zeros
>>> masker = gemmi.SolventMasker(gemmi.AtomicRadiiSet.Constant, 1.75)
>>> masker.set_to_zero(grid, st[0])
>>>
>>> # find the blob
>>> blobs = gemmi.find_blobs_by_flood_fill(grid, cutoff=0.6, min_volume=5,
...                                        min_score=0, min_peak=0)
>>> blobs  
[<gemmi.Blob object at 0x...>]
>>> blobs[0].volume
9.967250538023837
>>> blobs[0].score  
10.18154...
>>> blobs[0].peak_value  
1.848643...
>>> blobs[0].centroid
<gemmi.Position(12.5868, -0.45056, 0)>
>>> blobs[0].peak_pos
<gemmi.Position(12.307, 0, 0)>

In addition to the blob coordinates, it can be useful to know what is the nearest chain, residue and atom. Here is a quick recipe how to find it out with the help of NeighborSearch:

>>> pos = blobs[0].peak_pos
>>> ns = gemmi.NeighborSearch(st[0], st.cell, 8).populate(include_h=False)
>>> mark = ns.find_nearest_atom(pos)
>>> mark.to_cra(st[0])
<gemmi.CRA A/GLN 303/O>
>>> # To calculate distance from the atom, we need to account for the periodicity
>>> # of crystal. mark.pos is atom.pos transformed by a symmetry op, but we may need
>>> # to add a multiplicity of the unit cell vectors before calculating the distance.
>>> st.cell.find_nearest_pbc_image(pos, mark.pos, 0)
<gemmi.NearestImage 1_554 in distance 3.51>
>>> # You may also want to find a symmetry image of the blob that is near
>>> # the original molecule.
>>> atom_pos = mark.to_cra(st[0]).atom.pos
>>> st.cell.find_nearest_pbc_position(atom_pos, pos, mark.image_idx, inverse=True)
<gemmi.Position(12.8665, -2.3885, 0)>
>>> _.dist(atom_pos)
3.511341999194701

Flood fill

Flood fill is an algorithm that determines the area connected to a seed point, the area of all connected points which match a certain condition. Here, the criterion for grid points is having the value above (or, alternatively, below) a given threshold value.

The blob search from the previous section uses flood fill and returns Blob objects that contain a few statistics for each blob. To get a mask corresponding to a Blob we need to run the flood fill algorithm again, using peak_pos as the seed:

>>> seed = blobs[0].peak_pos
>>> mask = gemmi.flood_fill_above(grid, [seed], threshold=0.6)
>>> mask
<gemmi.Int8Grid(90, 8, 30)>

The second argument of flood_fill_above() is a list of positions used as seeds. We could use multiple seeds to obtain a single mask for all blobs together.

To find area with values below a certain value, run flood_fill_above() with optional argument negate=True.

Here we print a few characteristics of the mask:

>>> mask.sum()  # == number of masked points
62
>>> _ * grid.unit_cell.volume / grid.point_count  # cf. blobs[0].volume
9.967250538023837
>>> extent = mask.get_nonzero_extent()  # bounding box containing the blob
>>> extent.minimum  # in fractional coordinates
<gemmi.Fractional(0.227778, -0.0625, -0.0833333)>
>>> grid.unit_cell.orthogonalize(extent.minimum)
<gemmi.Position(11.7177, -0.298563, -1.20317)>
>>> grid.unit_cell.orthogonalize(extent.maximum)
<gemmi.Position(13.4558, 4.47844, 1.20317)>

MRC/CCP4 maps

We support one file format for storing the grid data on disk: MRC/CCP4 map. The content of the map file is stored in a class that contains both the Grid class and all the meta-data from the CCP4 file header.

The CCP4 format has a few different modes that correspond to different data types. Gemmi supports:

• mode 0 – which corresponds to the C++ type int8_t,

• mode 1 – corresponds to int16_t,

• mode 2 – float,

• and mode 6 – uint16_t.

CCP4 programs use mode 2 (float) for the electron density, and mode 0 (int8_t) for masks. A mask is 0/1 data that marks a part of the volume, such as the solvent region. Other modes are not used in crystallography, but may be used for CryoEM data.

The CCP4 format is quite flexible. The data is stored as sections, rows and columns that correspond to a permutation of the X, Y and Z axes as defined in the file header. The file can contain only a part of the asymmetric unit or more than one asymmetric unit (i.e., redundant data). Typically, a span of the crystallographic map is one of the following:

• Covering a molecule with some margin around it. This is necessary for programs such as PyMOL that don’t know about symmetry. CCP4 utilities fft + mapmask can make such a map.

• Covering the asymmetric unit (asu). The program that reads the map is supposed to expand the symmetry. This approach is used by the CCP4 clipper library and by programs such as Coot.

The latter approach generates map for exactly one asu, if possible. It is not possible if the shape of the asu in fractional coordinates is not rectangular, and in such case we must have some redundancy. On average, the maps generated for asu are significantly smaller, as compared in the UglyMol wiki.

Nowadays, the CCP4 format is rarely used in crystallography. Almost all programs read the reflection data and calculate maps on the fly.

The MRC variant of the format contains the ORIGIN header records (words 50-52) that specify the location (in Angstroms) of a subvolume taken from a larger volume. Gemmi functions ignore this header because our focus was on crystallographic applications. Using it is up for discussion.

Reading

C++

To work with CCP4 maps you need:

#include <gemmi/ccp4.hpp>

The Ccp4 class is templated with the data type. Normally, we use float type for a map:

gemmi::Ccp4<float> map;
map.read_ccp4_map("my_map.ccp4");

and int8_t for a mask (mask typically has only values 0 and 1, but in principle the values can be from -127 to 128):

gemmi::Ccp4<int8_t> mask;
mask.read_ccp4_map("my_mask.ccp4");

If the grid data type does not match the file data type, the library will attempt to convert the data when reading.

Alternatively, you can use helper functions read_ccp4_map() and read_ccp4_mask() defined in gemmi/read_map.hpp.

Python

To read a ccp4 map:

>>> m = gemmi.read_ccp4_map('../tests/5i55_tiny.ccp4')
>>> m
<gemmi.Ccp4Map with grid 8x6x10 in SG #4>

Similarly, to read a mask (ccp4 map in mode 0) call read_ccp4_mask().

Header

The CCP4 map header is organised as 56 words (4-bytes that are interpreted as integer, float or 4 characters) followed by 800 bytes – a space for ten 80-character text labels.

Low-level access to the header is provided by getters and setters that use the word number (as in the format description from ccp4 or ccp-em) as the first argument.

C++

int32_t header_i32(int w) const;
float header_float(int w) const;
// ccp4 map header has mostly 80-byte strings
std::string header_str(int w, size_t len=80) const;

void set_header_i32(int w, int32_t value);
void set_header_float(int w, float value);
void set_header_str(int w, const std::string& str);

For example:

int mode = map.header_i32(4);
float x = map.header_float(11);

Python

>>> m.header_float(20), m.header_float(21)  # dmin, dmax
(-0.5310382843017578, 2.3988280296325684)
>>> m.header_i32(28)
0
>>> m.set_header_i32(28, 20140)
>>> m.header_str(57, 80).strip()
'Created by MAPMAN V. 080625/7.8.5 at Wed Jan 3 12:57:38 2018 for A. Nonymous'

When the file is read, the header is used to set properties of the grid:

>>> m.grid  # tiny grid as it is a toy example
<gemmi.FloatGrid(8, 6, 10)>
>>> m.grid.spacegroup
<gemmi.SpaceGroup("P 1 21 1")>
>>> m.grid.unit_cell
<gemmi.UnitCell(29.45, 10.5, 29.7, 90, 111.975, 90)>

setup()

read_ccp4_map() and read_ccp4_mask() read the data from file into a Grid class, by default keeping the same axis order and the same dimensions as in the file. But the functions that operate on the grid data (such as get_position(), interpolate_value(), symmetrize()) expect that the grid covers the whole unit cell and that the axes are in the X,Y,Z order. So before calling a function that uses either the symmetry or the unit cell parameters we need to setup the grid as required. You do this either by calling the reading function with the optional argument setup=True, or by calling the setup() method afterwards.

The setup function has two arguments. The first one is a value to be used for unknown values. It is used only when the input file does not cover a complete asymmetric unit. (If you used CCP4 program MAPMASK – it is keyword PAD there). When you call a read function with setup=True, this argument is NaN for maps and -1 for masks.

The second argument (mode) is optional and can be used to perform a partial setup.

• MapSetup.Full – (default value) reorders and resizes the grid to cover the whole unit cell, applying symmetry.

• MapSetup.NoSymmetry – does not use symmetry operations, only cell repeat (periodic boundary conditions, PBC) when extending the map.

• MapSetup.ReorderOnly – only reorders axes to X, Y, Z.

C++

map.setup(NAN);

Python

>>> m.setup(float('nan'))
>>> # the grid dimensions were 8x6x10, now they are:
>>> m.grid
<gemmi.FloatGrid(60, 24, 60)>

Non-default modes are only for special occasions. For example, if we had a suspicious file and wanted to check if the map values obey the symmetry specified in the file, we could do this:

  >>> m = gemmi.read_ccp4_map('../tests/5i55_tiny.ccp4')
  >>> m.setup(float('nan'), mode=gemmi.MapSetup.NoSymmetry)
  >>> grid_copy = m.grid.clone()
  >>> # use two grids to store min and max values of symmetry mates
  >>> m.grid.symmetrize_min()
  >>> grid_copy.symmetrize_max()
  >>> # find the biggest difference between symmetry-related points
  >>> numpy.nanmax(grid_copy.array - m.grid.array)
  0.0

Writing

To write a map to a file, update the header if necessary, (optionally) set the extent of the map that is to be written, and call write_ccp4_map().

map.update_ccp4_header();
// map.set_extent(...);
map.write_ccp4_map(filename);

>>> m.update_ccp4_header()
>>> # m.set_extent(...)
>>> m.write_ccp4_map('out.ccp4')

update_ccp4_header() does the following:

• if the map header is empty (a new map was created): it prepares the header,

• if the optional argument mode is given and if it is different than the current mode: the mode is changed and the data type will be converted while writing the file; the mode can be 0, 1, 2, 6, or -1 (default – no action),

• if the optional argument update_stats is true (the default is true): DMIN, DMAX, DMEAN and RMS in the map header are re-calculated.

By default, the written map covers the whole unit cell. To change this, call set_extent() before writing the map. As an example, let us cover a molecule with 5Å margin (equivalent of running CCP4 program MAPMASK with XYZIN and BORDER 5).

map.set_extent(calculate_fractional_box(structure, 5));

>>> st = gemmi.read_structure('../tests/5i55.cif')
>>> m.set_extent(st.calculate_fractional_box(margin=5))
>>> m.write_ccp4_map('out.ccp4')

After calling set_extent() we have the same situation as before calling setup() – some grid functions may not work correctly.

Here we show three other scenarios of setting the map extent.

You may want to preserve the original map extent, which can be read by calling get_extent() before the setup:

>>> m = gemmi.read_ccp4_map('../tests/5i55_tiny.ccp4')
>>> box = m.get_extent()
>>> m.setup(float('nan'))
>>> # ... here the map gets modified ...
>>> m.set_extent(box)
>>> m.write_ccp4_map('out.ccp4')

Alternatively, you may want to write only an asymmetric unit (actually, asu brick) of the map, which is enough to calculate the density everywhere. For this, use the brick extent:

>>> brick = gemmi.find_asu_brick(m.grid.spacegroup)
>>> brick.str()
'0<=x<=1/2; 0<=y<1; 0<=z<1'
>>> box = brick.get_extent()

At last, if the map would be padded with zeros or NaNs you could determine the box that contains real data with get_nonzero_extent():

>>> m = gemmi.read_ccp4_map('../tests/5i55_tiny.ccp4')
>>> m.setup(0., gemmi.MapSetup.NoSymmetry)
>>> m.grid.get_nonzero_extent()  
<gemmi.FractionalBox object at 0x...>

Map from Grid

To write grid data as a ccp4 file: create a new Ccp4 class, set the grid, call update_ccp4_header() and write the file.

>>> ccp4 = gemmi.Ccp4Map()
>>> ccp4.grid = gemmi.FloatGrid(numpy.zeros((10, 10, 10), dtype=numpy.float32))
>>> ccp4.grid.unit_cell.set(20, 20, 20, 90, 90, 90)
>>> ccp4.grid.spacegroup = gemmi.SpaceGroup('P1')
>>> ccp4.update_ccp4_header()
>>> ccp4.write_ccp4_map('out.ccp4')

Maps are often calculated from map coefficients – example in section about FFT shows how to calculate such a map and write it to a file.

Examples

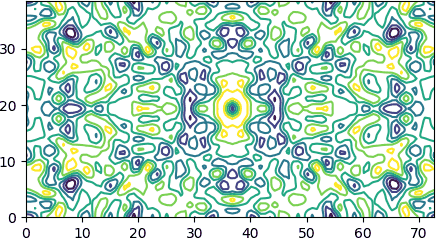
Example 1. A short code that draws a contour plot similar to mapslicer plots (see Fig. 3 in this CCP4 paper if you wonder what is mapslicer). To keep the example short we assume that the lattice vectors are orthogonal.

import numpy
from matplotlib import pyplot
import gemmi

# toxd_aupatt.map is generated by $CCP4/examples/unix/runnable/patterson
ccp4 = gemmi.read_ccp4_map('/tmp/wojdyr/toxd_aupatt.map', setup=True)
arr = numpy.array(ccp4.grid, copy=False)
x = numpy.linspace(0, ccp4.grid.unit_cell.a, num=arr.shape[0], endpoint=False)
y = numpy.linspace(0, ccp4.grid.unit_cell.b, num=arr.shape[1], endpoint=False)
X, Y = numpy.meshgrid(x, y, indexing='ij')
pyplot.contour(X, Y, arr[:,:,40])
pyplot.gca().set_aspect('equal', adjustable='box')
pyplot.show()

Example 2. A tiny utility that compares two masks (maps with 0/1 values) of the same size, printing a summary of matches and mismatches:

$ python examples/maskdiff.py old_mask.ccp4 new_mask.ccp4
Size: 240 x 300 x 270  and  240 x 300 x 270
0-0      5006818  25.76%
1-1     13496058  69.42%
0-1       937124   4.82%
1-0            0   0.00%
total   19440000

Here is the script:

import sys
import numpy
import gemmi

def maskdiff(path1, path2):
    mask1 = gemmi.read_ccp4_mask(path1, setup=True)
    arr1 = numpy.array(mask1.grid, copy=False)
    mask2 = gemmi.read_ccp4_mask(path2, setup=True)
    arr2 = numpy.array(mask2.grid, copy=False)
    print("Size: %d x %d x %d  and  %d x %d x %d" % (arr1.shape + arr2.shape))
    if arr1.shape != arr2.shape:
        sys.exit("Different sizes. Exiting.")
    t = 2 * (arr1 != 0) + (arr2 != 0)
    for (a, b) in [(0, 0), (1, 1), (0, 1), (1, 0)]:
        n = numpy.count_nonzero(t == 2*a+b)
        print('%d-%d %12d %6.2f%%' % (a, b, n, 100.*n/arr1.size))
    print('total %10d' % arr1.size)

if __name__ == '__main__':
    if len(sys.argv) != 3:
        sys.exit("Usage: maskdiff.py map1 map2")
    maskdiff(sys.argv[1], sys.argv[2])